STEM-Plus Content offers K-12 math and other STEM content in both English and Japanese.
The content aids in vocabulary acquisition for both English and Japanese learners.
How does it achieve this?
Through the content, learners grasp words and phrases more intuitively because they already know their meanings in their native language.
It is like learning the word “apple” by looking at a picture of one.
STEM-Plus Content facilitates easy learning of abstract yet useful words.
To ensure effective and efficient learning, the content is designed to be concise and illustrative.
Learners can easily understand the material through images and examples.
In addition, the content provides useful tips on math and other STEM subjects, supporting
academic success in these important fields.
How to use:
Carefully selected English words and phrases related to “Circles and Arcs” are highlighted in yellow in the images below. The words are also summarized at the bottom of this page.
We recommend reviewing them regularly during your daily math studies to enhance your vocabulary.
TERMS, DEFINITIONS, AND ILLUSTRATIONS
Circles
- A circle is the set of all points that are equidistant from a given point called the center of the circle.
円とは与えられた点(中心とよぶ)から等距離にあるすべての点の集合のこと。 - A radius is a segment form the center of the circle to any point of the circle.
半径とは中心から円のいずれかの点への線分のこと。 - A chord is a segment whose endpoints are points on the circle.
弦とは(ふたつの)終点が円の(ふたつの)点である線分のこと。 - A diameter is a chord that passes through the center of the circle.
直径とは中心を通る弦のこと。 - The terms radius and diameter describe measures as well as segments.
半径と直径という用語は、線分(それ自体)だけでなく長さも言い表す(ことがある)。
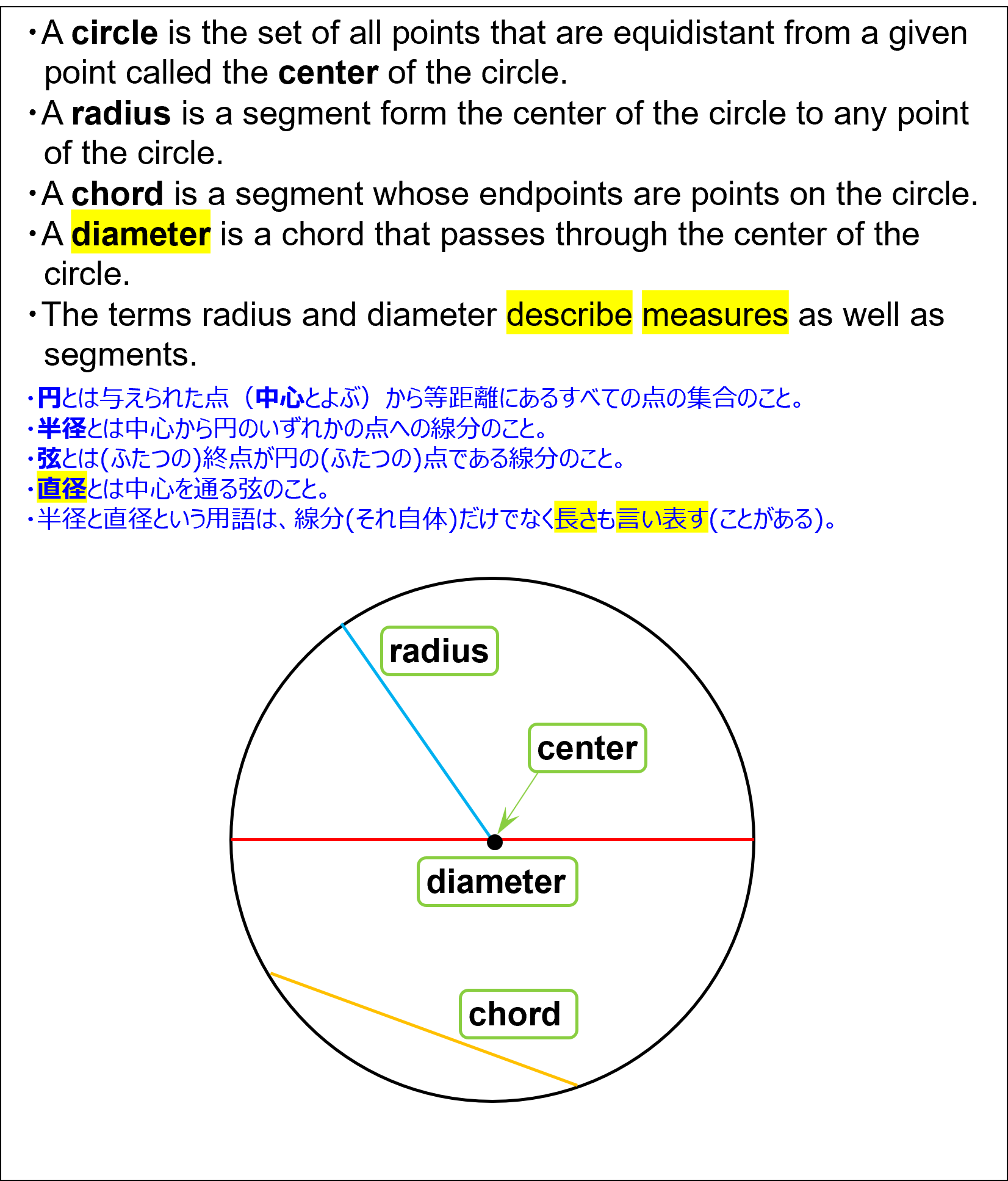
Circles
Circles and Lines (Tangents, etc.)
- A secant is a line that intersects a circle in two points.
割線とは円とふたつの点で交わる直線のこと。 - A tangent is a line in the plane of a circle that intersects the circle in exactly one point, the point of tangency.
接線とは円とちょうどひとつの点(接点)で交わる円を含む平面上の直線のこと。
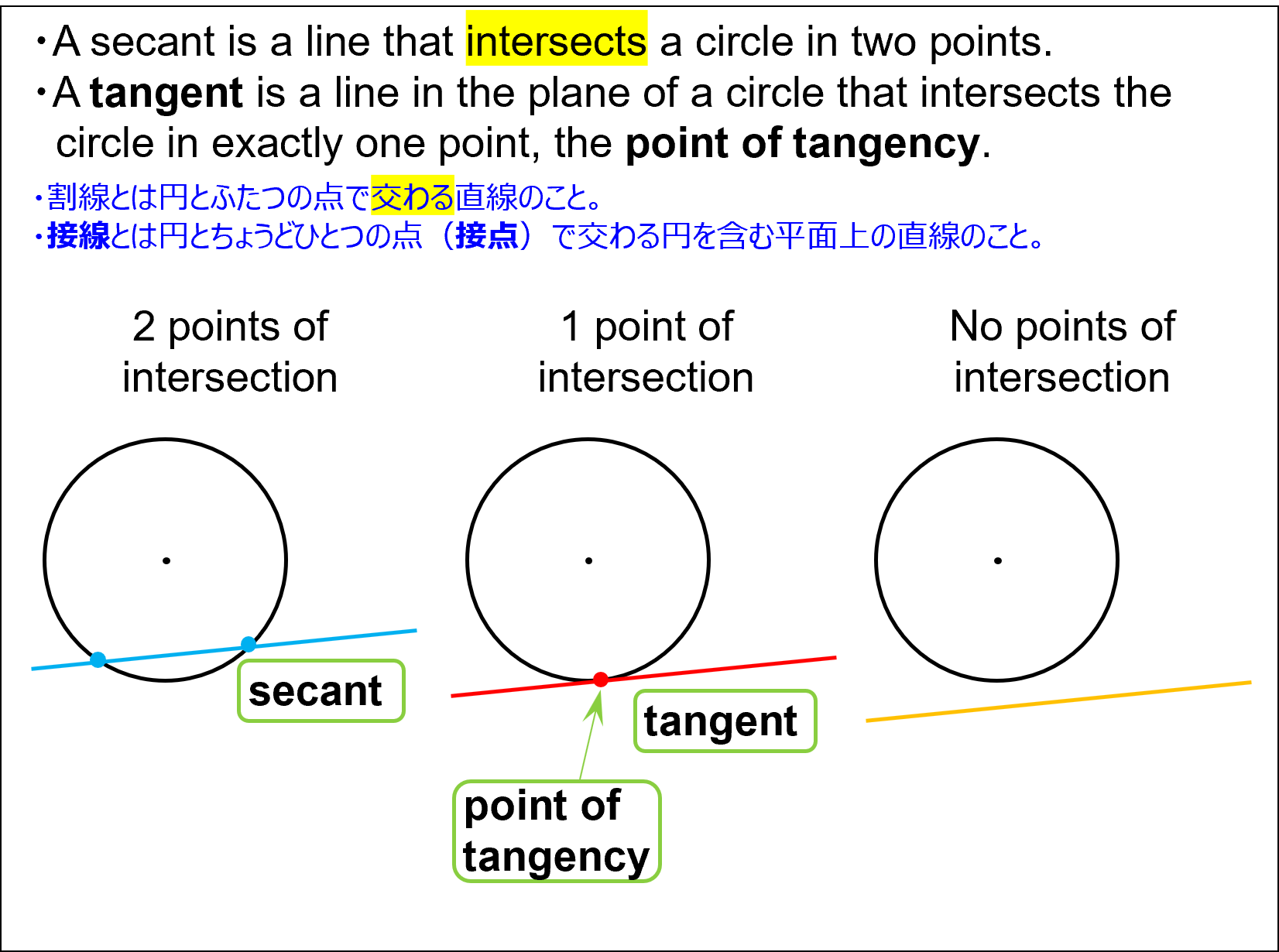
Circles and Tangents
Circles and Circles (Internal Tangency, etc.)
- Coplanar circles that intersect in one point are called tangent circles.
ひとつの点で交わる同一平面上の円(複数)を相接する円とよぶ。 - Coplanar circles that have a common center are called concentric circles.
共通の中心をもつ同一平面上の円(複数)を同心円とよぶ。 - Internally tangent / Externally tangent
内接する / 外接する
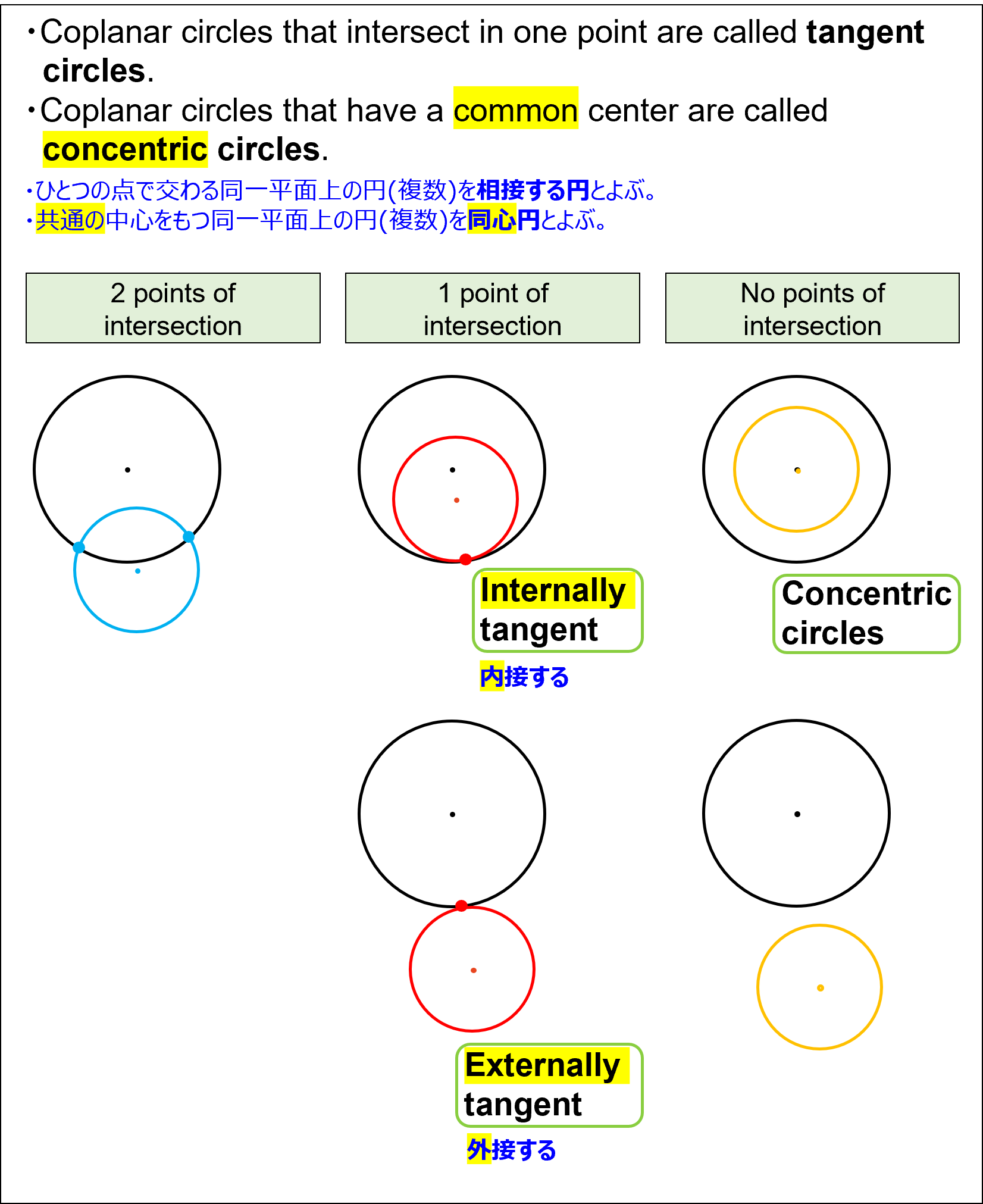
Coplanar Circles
Arcs and Measurement
- An arc of a circle is two points on the circle and the continuous part of the circle between the two points.
円の弧とは円上のふたつの点とそれらの間の円の連続した部分のこと。 - A central angle of a circle is an angle whose vertex is the center of the circle.
円の中心角とはその頂点が円の中心である角のこと。 - Measuring Arcs
弧の計量- The measure of an arc is defined to be the measure of its central angle.
弧の大きさとはその中心角の大きさと定義される。 - The expression m(AB) is read as “the measure of arc AB.”
表記m(AB)は「弧ABの大きさ」とよむ。 - The measure of the entire circle is 360°. The measure of a semicircle is 180°.
円全体での大きさは360°。 半円での大きさは180°。
- The measure of an arc is defined to be the measure of its central angle.
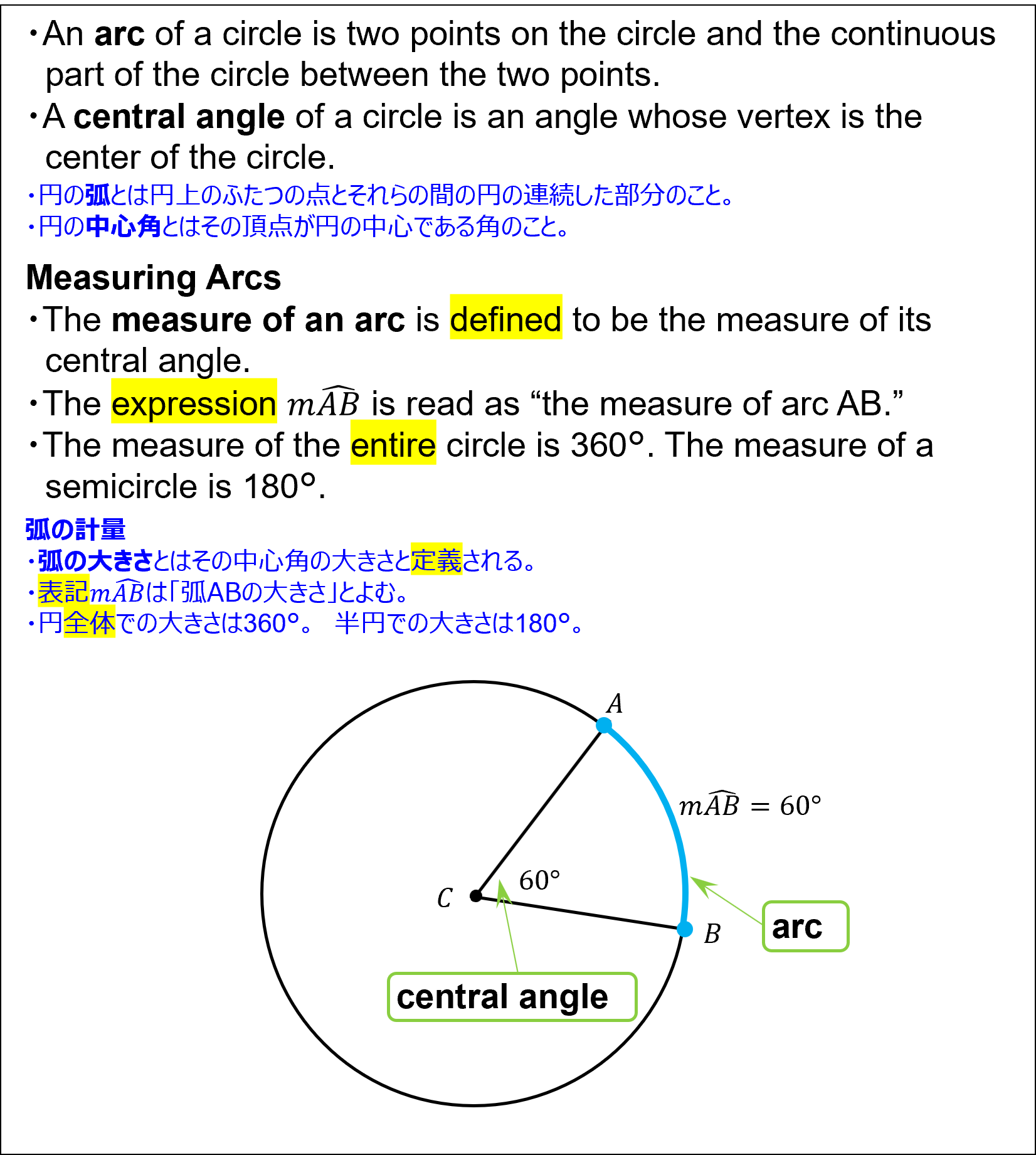
Measuring Arcs
Circumference and Arc Length
- The distance around a circle is called the circumference.
円のまわりの距離を円周(周長)とよぶ。 - For every circle, the ratio of the circumference to the diameter is close to 3.14.
The Greek letter π (pi) is used to represent this ratio.
各々の円について直径に対する円周の比は3.14に近い。
この比を表すのにギリシア文字のπ(パイ)が使われる。 - The circumference C of a circle is the product of π and the diameter d, or twice the product of π and the radius r.
円の周長Cはπと直径dの積、またはπと半径rの積の2倍。 - An arc length is a portion of the circumference of a circle.
弧長とは円の周長の一部分のこと。 - The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to 360°.
弧の長さの周長に対する比は、その弧の大きさの360°に対する比に等しい。

Circumference and Arc Length
Area of Circles and Sectors
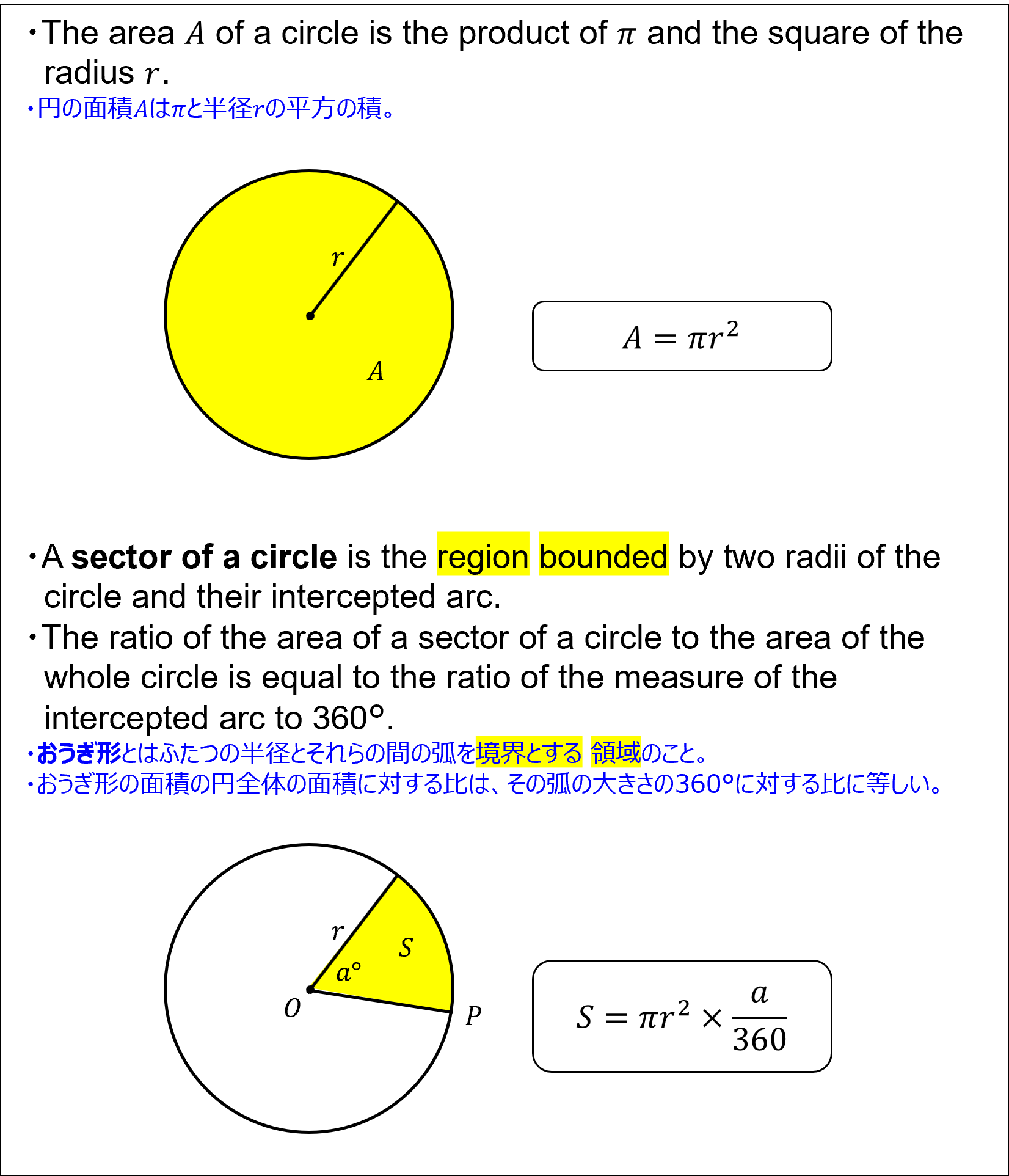
- The area A of a circle is the product of π and the square of the radius r.
円の面積Aはπと半径rの平方の積。 - A sector of a circle is the region bounded by two radii of the circle and their intercepted arc.
おうぎ形とはふたつの半径とそれらの間の弧を境界とする 領域のこと。 - The ratio of the area of a sector of a circle to the area of the whole circle is equal to the ratio of the measure of the intercepted arc to 360°.
おうぎ形の面積の円全体の面積に対する比は、その弧の大きさの360°に対する比に等しい。
Areas of Circles and Sectors
WORDS AND PHRASES
✅diameter 直径
✅describe を言い表す
✅measure 大きさ;測定単位;対策/を測る、長さなどを見つける;を評価する
✅intersection 交差点;交差
📎intersect (と)交差する/交差
✅concentrate 集中する{注意など};集結する{場所}
📎concentric 中心が同じ
✅internal 内部の;国内の;体内の
✅external 外部の;外国の;外的な
✅common 共通の;普通の
✅define を定義する;を特徴づける
✅express を表現する
📎expression 表現
✅entire 完全な、全部の
✅distance 距離{2点の間の空間の大きさ}
✅length 長さ{物の両端の間や時間の}
✅portion 部分;{食事の}一人前;{責任などの}割当て
✅region 領域;地域
✅boundary 境界
📎bound {be bounded by A}Aを境界とする;跳ねる;bind(縛る)の過去・分詞
TIPS
Making the most of ‘Tangent’
The term ‘tangent’ is used to refer to the trigonometric function ‘tan’ (tangent) as well as to mean a line that intersects a circle in exactly one point (‘tangent line’). Interestingly, the ‘tan’ function actually relates to the length of a tangent line. What am I talking about? Look forward to high school mathematics.
By the way, the etymological meaning of ‘tangent’ is ‘to touch,’ and the word ‘tangible’ comes from the same root. The term ‘tangible’ is frequently used in various professional contexts. It’s a good idea to learn these terms simultaneously, making the most of this opportunity.
✅tangible {目に見えて}明らかな;触れられる
tangible assets 有形資産、intangible assets 無形資産


