STEM-Plus Content offers K-12 math and other STEM content in both English and Japanese.
The content aids in vocabulary acquisition for both English and Japanese learners.
How does it achieve this?
Through the content, learners grasp words and phrases more intuitively because they already know their meanings in their native language.
It is like learning the word “apple” by looking at a picture of one.
STEM-Plus Content facilitates easy learning of abstract yet useful words.
To ensure effective and efficient learning, the content is designed to be concise and illustrative.
Learners can easily understand the material through images and examples.
In addition, the content provides useful tips on math and other STEM subjects, supporting
academic success in these important fields.
How to use:
Carefully selected English words and phrases related to “Construction Basics” are highlighted in yellow in the images below. The words are also summarized at the bottom of this page.
We recommend reviewing them regularly during your daily math studies to enhance your vocabulary.
TERMS, DEFINITIONS, AND ILLUSTRATIONS
Construction
- A construction is a geometric drawing that uses only a compass and a straightedge.
作図とはコンパスと定規だけを使う幾何的な製図のこと。 - A straightedge is used to draw a line segment but is not used to measure distance.
定規は線分をかくために使われるが、距離を測定するためには使われない。 - A compass is used to draw circles or arcs of circles to locate points at a fixed distance from given point.
コンパスは円をかいたり、与えられた点から一定の距離にある点(複数)の位置を見つけるための弧をかくために使われる。

Construction
Copying a Segment
- Copying a Segment
線分のコピー- Use the following steps to construct a segment that is congruent to AB.
線分ABと等しい線分を作図するには、以下のステップをたどる。- Draw a segment longer than AB.
ABより長い線分をかく。 - Measure the length of AB.
ABの長さを測る。 - Using the same radius, draw an arc with center C.
同じ半径を使って、Cを中心に弧をかく。
- Draw a segment longer than AB.
- Use the following steps to construct a segment that is congruent to AB.
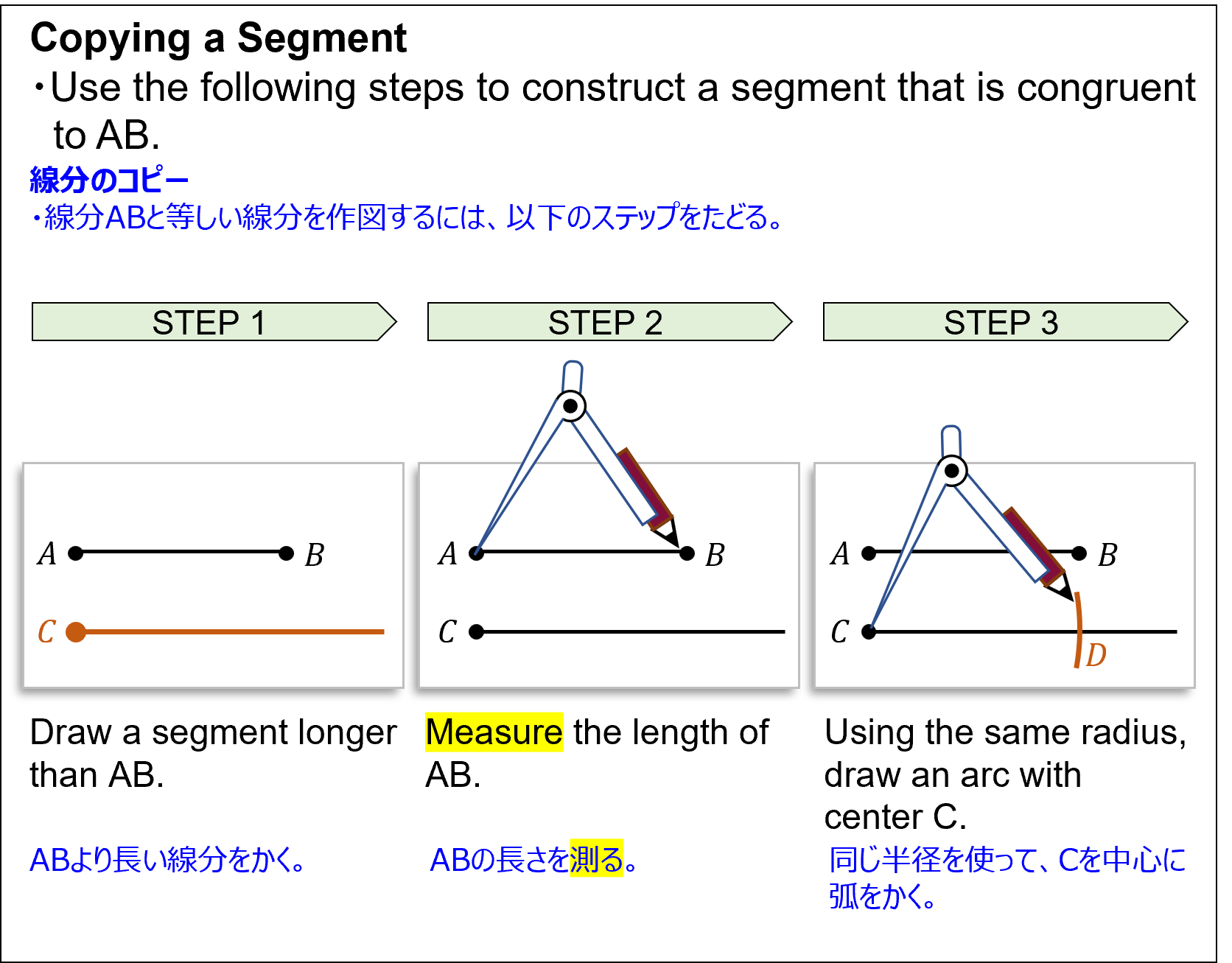
Copying a Segment
Copying an Angle
- Copying an Angle
角のコピー- Use the following steps to construct an angle that is congruent to ∠A.
∠Aと等しい角を作図するには、以下のステップをたどる。- Draw a segment.
線分をかく。 - Draw an arc with center A. Using the same radius, draw an arc with center D.
Aを中心に弧をかく。同じ半径を使って、Dを中心に弧をかく。 - Measure the length of BC. Draw an arc with radius BC and center E.
BCの長さを測る。Eを中心に半径BCの弧をかく。 - Draw DF.
DFをかく。
- Draw a segment.
- Use the following steps to construct an angle that is congruent to ∠A.
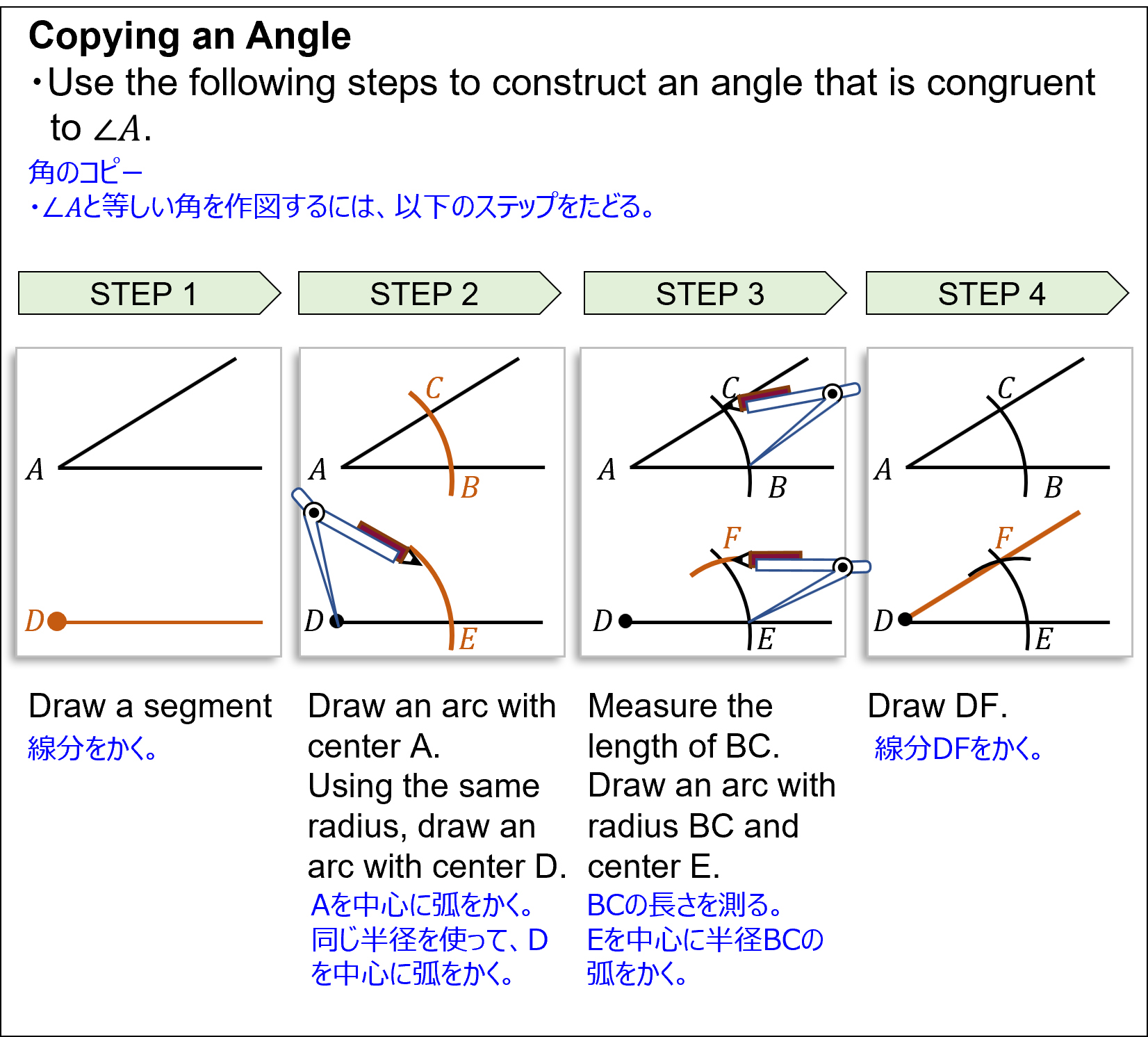
Copying an Angle
Segment Bisector
- Segment Bisector
線分の二等分線- The midpoint of a segment is the point that divides the segment into two congruent segments.
線分の中点とはその線分を2つの等しい線分にわける点のこと。 - A segment bisector is any line that passes through the midpoint of a segment.
線分の二等分線とはその線分の中点を通る直線のこと。 - If a segment bisector is also perpendicular to the segment, it is called the perpendicular bisector of the segment.
線分の二等分線がその線分に垂直でもある場合は、その線分の垂直二等分線とよぶ。
- The midpoint of a segment is the point that divides the segment into two congruent segments.

Segment Bisector
Constructing a Segment Bisector
- Bisecting a Segment
線分の二等分- Use the following steps to construct a bisector of AB.
線分ABの二等分線を作図するには、以下のステップをたどる。- Use a compass setting greater than one-half of AB. Place the compass at A. Draw an arc above AB and an arc below AB.
ABの半分より長くコンパスをセットする。Aにコンパスを合わせる。ABの上と下に弧をかく。 - Using the same radius, place the compass at B. Draw an arc above AB and an arc below AB.
同じ半径を使って、Bにコンパスを合わせる。ABの上と下に弧をかく。 - Draw CD.
CDをかく。
- Use a compass setting greater than one-half of AB. Place the compass at A. Draw an arc above AB and an arc below AB.
- Use the following steps to construct a bisector of AB.
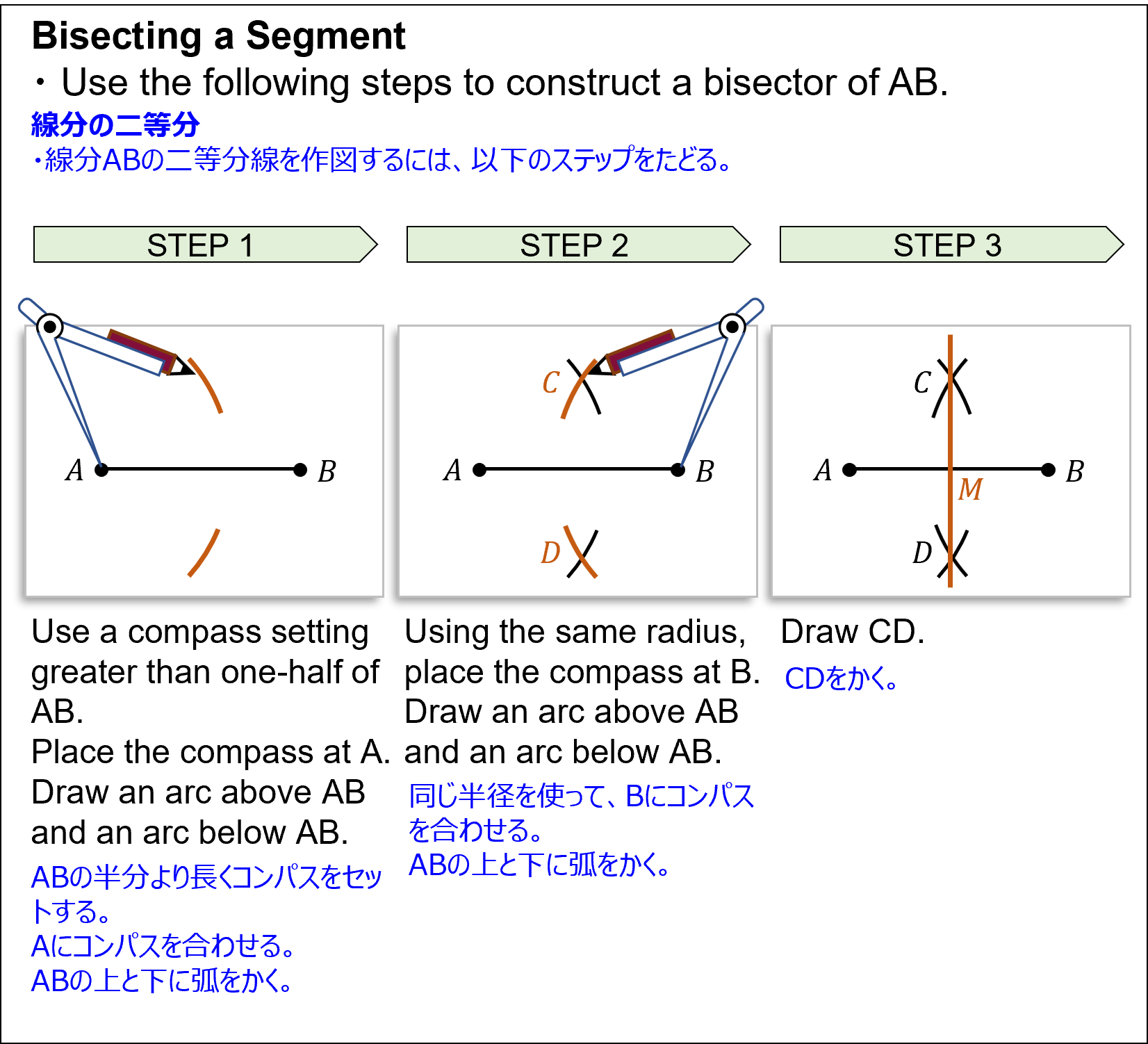
Bisecting a Segment
Constructing an Angle Bisector
- Angle Bisector
角の二等分- An angle bisector is the ray that divides a given angle into two congruent angles.
角の二等分線とは与えられた角を2つの等しい角にわける半直線のこと。
- An angle bisector is the ray that divides a given angle into two congruent angles.
- Bisecting an Angle
角の二等分- Use the following steps to construct an angle bisector of ∠A.
∠Aの二等分線を作図するには、以下のステップをたどる。- Draw an arc with center A.
Aを中心に弧をかく。 - With C as a center, draw an arc in the interior of ∠A.
Cを中心に、 ∠の内側に弧をかく。 - Using the same radius, draw an arc with center B.
同じ半径を使って、Bを中心に弧をかく。 - Draw AD.
ADをかく。
- Draw an arc with center A.
- Use the following steps to construct an angle bisector of ∠A.
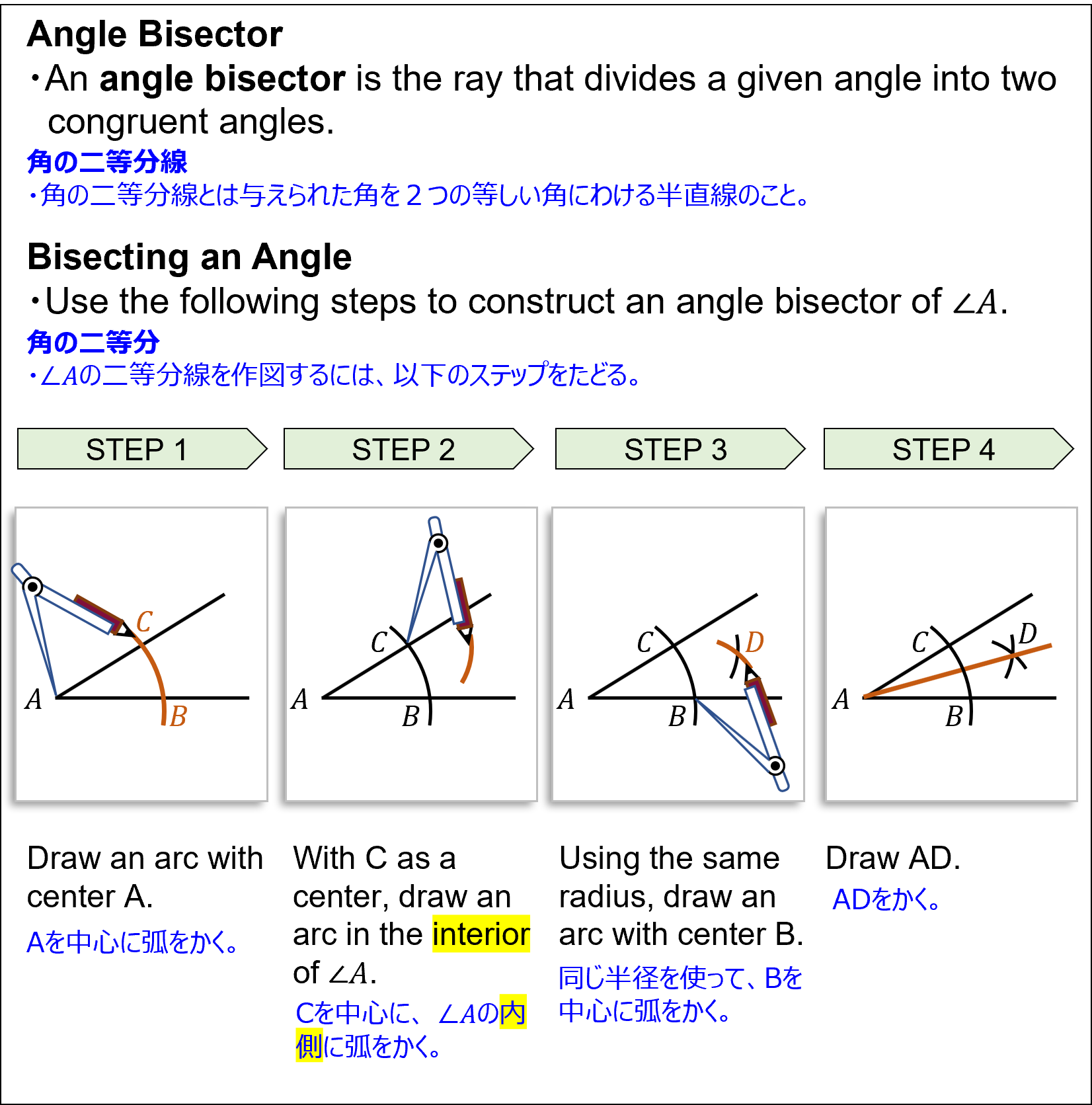
Bisecting an Angle
WORDS AND PHRASES
✅construct {建物}を建設する;{文・議論など}を構成する
📎construction 構造(物);作図
✅segment 部分
/を分割する
✅locate の位置を見つける;[受動]に位置付ける
✅measure を測る、長さなどを見つける;を評価する
/対策;測定単位
✅divide をわける;をわる
/分割;分裂
✅interior 内部・内側
/内側の・室内の ⇔ exterior
TIPS
Understanding the ‘Sec/Seg’ Root
The root ‘seg’ or ‘sec’ in words like ‘segment’ or ‘bisect’ means ‘to cut.’
Later in the math curriculum, we will explore ‘sectors’ (おうぎ形, 部門).
Learning these words collectively is an effective strategy, and you can even include related words such as ‘sect’ (派閥), ‘section’ (節、項), and ‘insect’ (昆虫).
Notes on Construction Steps
A compass is used to draw circles, of course. In addition, as mentioned above, it’s also used ‘to draw arcs of circles to locate points at a fixed distance from a given point.’ While this explanation may seem obvious, it gives a fundamental way of understanding how a compass is used in constructions such as bisecting segments.
In ‘Copying an Angle,’ the angle is considered as a part of a triangle, and by copying the triangle (constructing a congruent triangle), the angle is copied. This step is an important foundation in learning how to construct congruent triangles.
Many textbooks address the tasks of (A) copying and (B) bisecting for both (1) segments and (2) angles. This approach facilitates an integrated understanding for learners.


